
geometry mid-year test study guide
Prepare thoroughly! This guide aids refocusing goals‚ revitalizing strategies‚ and mastering foundational concepts like points‚ lines‚ angles‚ and triangle properties for success․
I․ Foundations of Geometry
Understanding the bedrock principles is crucial․ This section revisits basic geometric figures – points‚ lines‚ and planes – defining their characteristics and relationships․ Mastery of segments‚ rays‚ and calculating distance using the distance formula is essential․
Focus on angle relationships: complementary‚ supplementary‚ vertical‚ and adjacent angles․ Practice identifying and applying these concepts in problem-solving․ Arakelov geometry‚ a generalization‚ builds upon these foundations‚ linking arithmetic schemes with Hermitian vector bundles․
Remember‚ a solid grasp of these foundational elements is paramount for tackling more complex geometric challenges later in the course․ Don’t treat this as a formality; it’s the base for everything else!
A․ Basic Geometric Figures
Visualize and define! This focuses on fundamental shapes: points (location‚ no dimension)‚ lines (one-dimensional‚ infinite extent)‚ line segments (part of a line with endpoints)‚ and rays (starting point‚ infinite in one direction)․
Understand planes (two-dimensional‚ infinite extent)․ Practice identifying these figures in diagrams and real-world examples․ Consider how these figures interact – lines intersecting planes‚ segments lying on lines․
Fast Geometry Streaming utilizes these basic shapes to efficiently load complex models․ Remember‚ nearly one in four business leaders view mid-year reviews as vital for refocusing goals‚ much like mastering these figures refocuses your geometric understanding․ Don’t let these basics collect dust!
B․ Points‚ Lines‚ and Planes
Fundamental building blocks! Deepen understanding of undefined terms: points (precise location)‚ lines (straight path‚ infinite length)‚ and planes (flat surface‚ infinite extent)․ Explore postulates relating these – through any two points‚ there’s exactly one line․
Understand how three non-collinear points define a unique plane․ Practice visualizing and sketching these elements․ Consider how these concepts relate to geometric modeling in software like CATIA‚ where precise definition is crucial․
Like a mid-year performance review‚ revisiting these basics revitalizes your foundation․ Arakelov geometry‚ a generalization‚ builds upon these concepts․ Remember‚ a strong grasp here streamlines more complex topics – a stable framework for geometric exploration․
C․ Segments‚ Rays‚ and Distance
Measuring space! Master defined terms derived from lines: segments (finite portion between two endpoints)‚ and rays (starting at one endpoint‚ extending infinitely)․ Understand the crucial distance formula – a cornerstone for calculating lengths․
Practice applying segment addition and subtraction postulates․ Visualize how these concepts translate into geometric modeling‚ like importing external geometry files into software․ Just as a mid-year review takes stock‚ accurately measuring these elements is vital․
Explore how these relate to concepts in more advanced fields like symplectic geometry‚ used in the three-body problem․ A solid understanding of distance is foundational‚ much like a stable frame rate in Fast Geometry Streaming within UE5․6․
D․ Angle Relationships
Decoding angles! Thoroughly review angle classifications (acute‚ obtuse‚ right‚ straight) and angle pairs: complementary (sum to 90°)‚ supplementary (sum to 180°)‚ vertical angles (congruent)‚ and adjacent angles․
Practice identifying these relationships in diagrams and applying them to solve for unknown angle measures․ Consider how these principles underpin geometric modeling in CATIA‚ where projecting 3D elements relies on precise angular definitions․
Just as a mid-year review refocuses goals‚ understanding angle relationships provides a crucial foundation․ Explore connections to advanced concepts like symplectic geometry and its role in understanding complex systems‚ mirroring the precision needed in software like ANSYS Workbench․

II․ Triangle Properties
Master triangles! Focus on theorems relating angle sums‚ exterior angles‚ and side lengths․ Understand inequalities and classify triangles by sides and angles effectively․
A․ Triangle Sum Theorem
Understanding the Core Concept: The Triangle Sum Theorem is a fundamental principle in geometry stating that the sum of the interior angles in any triangle always equals 180 degrees․ This seemingly simple theorem forms the basis for numerous calculations and proofs involving triangles; It’s crucial to not only memorize the theorem but also understand why it works – visualizing how angles combine to form a straight line can be incredibly helpful․
Applying the Theorem: Practice problems will likely involve finding a missing angle when two angles are known․ You might also encounter problems where you need to set up an algebraic equation to solve for an unknown angle measure․ Be prepared to apply the theorem in conjunction with other geometric principles‚ such as vertical angles or supplementary angles․
Common Pitfalls: A frequent mistake is assuming the theorem applies to all polygons‚ not just triangles․ Also‚ carefully identify the angles that are actually interior angles of the triangle – diagrams can sometimes be misleading․ Review examples and practice consistently to solidify your understanding and avoid these common errors․
B․ Exterior Angle Theorem
Defining Exterior Angles: An exterior angle of a triangle is formed by extending one side of the triangle․ It’s supplementary to the adjacent interior angle․ The Exterior Angle Theorem states that the measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles․ This theorem provides a powerful tool for finding unknown angle measures․
Practical Applications: Test questions will likely present diagrams requiring you to identify exterior angles and use the theorem to calculate their measures․ You may need to combine the Exterior Angle Theorem with the Triangle Sum Theorem to solve more complex problems․ Understanding the relationship between interior and exterior angles is key․
Avoiding Confusion: Be careful not to confuse an exterior angle with an interior angle․ Always identify the two non-adjacent interior angles correctly when applying the theorem․ Practice visualizing the relationship between angles and consistently work through example problems to build confidence and accuracy․
C․ Triangle Inequality Theorem
The Core Principle: The Triangle Inequality Theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side․ This seemingly simple rule is fundamental to determining whether three given side lengths can actually form a valid triangle․
Applying the Theorem: On your mid-year test‚ expect problems presenting three side lengths and asking if a triangle can be constructed․ You’ll need to test all three possible combinations of side additions․ If any combination fails to satisfy the inequality (a + b > c‚ a + c > b‚ b + c > a)‚ then a triangle cannot be formed․
Real-World Relevance & Problem Solving: This theorem isn’t just abstract; it reflects the physical constraints of triangle construction․ Practice identifying invalid triangle combinations and understanding why they don’t work․ Mastering this concept will significantly boost your problem-solving skills․
D․ Types of Triangles (Scalene‚ Isosceles‚ Equilateral)
Classifying by Sides: Triangles are categorized based on their side lengths․ Scalene triangles have all three sides of different lengths‚ resulting in all angles being unequal․ Isosceles triangles possess two sides of equal length‚ and consequently‚ two equal angles (base angles)․ Equilateral triangles are defined by all three sides being congruent‚ leading to three equal angles‚ each measuring 60 degrees․
Key Properties & Test Focus: Your mid-year test will likely require you to identify triangle types given side lengths or angle measures․ Remember that an equilateral triangle is also an isosceles triangle (it just meets the stricter criteria for equilateral)․
Problem Solving Strategies: Practice applying the definitions․ If a problem states two angles are congruent‚ immediately consider an isosceles triangle․ Understanding these classifications is crucial for further geometric proofs and calculations․

III․ Congruence and Similarity
Master these concepts! Focus on SSS‚ SAS‚ ASA‚ AAS for congruence‚ and AA‚ SSS‚ SAS for similarity – vital for problem-solving success․
A․ Congruent Triangles (SSS‚ SAS‚ ASA‚ AAS)
Understanding congruent triangles is fundamental․ Two triangles are congruent if all corresponding sides and angles are equal․ This section focuses on the postulates used to prove congruence without needing to demonstrate all six equalities․
SSS (Side-Side-Side): If three sides of one triangle are congruent to three sides of another‚ the triangles are congruent․
SAS (Side-Angle-Side): If two sides and the included angle of one triangle are congruent to the corresponding parts of another‚ the triangles are congruent․
ASA (Angle-Side-Angle): If two angles and the included side of one triangle are congruent to the corresponding parts of another‚ the triangles are congruent․
AAS (Angle-Angle-Side): If two angles and a non-included side of one triangle are congruent to the corresponding parts of another‚ the triangles are congruent․
Practice identifying these postulates in diagrams and applying them in proofs․ Knowing when to use each postulate is key to efficient problem-solving․
B․ Corresponding Parts of Congruent Triangles (CPCTC)
CPCTC – Corresponding Parts of Congruent Triangles are Congruent – is a crucial theorem used after proving triangles congruent․ It’s not a postulate to prove congruence‚ but a justification to conclude that specific angles or sides are congruent because the triangles have already been proven congruent․
Once you’ve established triangle congruence using SSS‚ SAS‚ ASA‚ or AAS‚ you can confidently state that any corresponding parts are also congruent․ For example‚ if ΔABC ≅ ΔDEF‚ then ∠A ≅ ∠D‚ side AB ≅ side DE‚ and so on․
CPCTC is frequently used within multi-step proofs to demonstrate additional congruencies‚ leading to further conclusions about the geometric figure․ Mastering its application is vital for tackling complex geometry problems․ Remember to always state the congruence first‚ then invoke CPCTC․
C․ Similar Triangles (AA‚ SSS‚ SAS)
Similar triangles have the same shape but different sizes․ Proving similarity is key to solving for unknown side lengths and angles․ There are three primary postulates to establish triangle similarity:
AA (Angle-Angle) Similarity: If two angles of one triangle are congruent to two angles of another triangle‚ the triangles are similar․
SSS (Side-Side-Side) Similarity: If the three sides of one triangle are proportional to the three sides of another triangle‚ the triangles are similar․
SAS (Side-Angle-Side) Similarity: If two sides of one triangle are proportional to two sides of another triangle‚ and the included angles are congruent‚ the triangles are similar․
Understanding these postulates allows you to determine if triangles are similar and apply proportional reasoning to solve geometric problems․ Remember to set up proportions correctly when using SSS and SAS․
D․ Triangle Proportionality Theorem
The Triangle Proportionality Theorem states that if a line parallel to one side of a triangle intersects the other two sides‚ then it divides those sides proportionally․ This means the ratio of the segments created on one side equals the ratio of the segments created on the other side․
A corollary to this theorem is that if three parallel lines intersect two transversals‚ then they divide the transversals proportionally․ These theorems are crucial for solving problems involving divided segments and similar triangles․
Be prepared to apply these concepts to find missing side lengths in triangles and to prove relationships between segments․ Understanding proportional reasoning is essential for mastering this topic․ Practice setting up and solving proportions accurately․

IV․ Quadrilaterals
Master quadrilateral properties! Focus on parallelograms‚ rectangles‚ rhombuses‚ squares‚ trapezoids‚ and kites – their angles‚ sides‚ and diagonals are key to success․
A․ Properties of Parallelograms
Understanding parallelograms is crucial․ These four-sided figures possess distinct characteristics vital for problem-solving․ Remember that opposite sides are both parallel and congruent․ This means they never intersect and are equal in length․
Furthermore‚ opposite angles within a parallelogram are also congruent – they have the same measure․ Consecutive angles‚ however‚ are supplementary‚ adding up to 180 degrees․ Diagonals bisect each other‚ meaning they intersect at their midpoints‚ creating equal segments․
Be prepared to apply these properties to find missing side lengths‚ angle measures‚ and to prove whether a quadrilateral is a parallelogram․ Practice identifying these characteristics in diagrams and utilizing them in proofs․ Knowing these properties will significantly boost your confidence on the mid-year test!
B․ Properties of Rectangles‚ Rhombuses‚ and Squares
These are specialized parallelograms! Rectangles build upon parallelogram properties with four right angles․ This means diagonals are congruent – they have the same length․ Rhombuses‚ also parallelograms‚ have four congruent sides․ Their diagonals are perpendicular bisectors of each other‚ forming right angles where they intersect․
Squares combine the best of both worlds: four right angles and four congruent sides․ Consequently‚ their diagonals are congruent‚ perpendicular bisectors․ Understanding these distinctions is key․
Expect problems requiring you to differentiate between these shapes based on given information․ Practice applying the Pythagorean theorem within rectangles and rhombuses․ Be prepared to utilize diagonal properties to solve for missing lengths and angles․ Mastering these nuances will prove invaluable on your geometry mid-year assessment!
C․ Trapezoids and Kites

Distinct quadrilaterals require unique approaches! Trapezoids possess only one pair of parallel sides – these are the bases․ An isosceles trapezoid has congruent non-parallel sides (legs) and congruent base angles․ Kites‚ conversely‚ have two pairs of adjacent congruent sides․ Their diagonals intersect at right angles‚ and one diagonal bisects the other․
Focus on identifying these shapes and applying their specific properties․ Expect problems involving finding missing angles or side lengths using geometric relationships․ Understanding the median of a trapezoid (the segment connecting the midpoints of the legs) is crucial․
Practice visualizing and manipulating these figures․ Don’t overlook the potential for using the Pythagorean theorem within right triangles formed by the diagonals and sides of kites․ A solid grasp of these concepts will significantly boost your performance on the mid-year exam!

V․ Circles
Master circle fundamentals! Understand radius‚ diameter‚ chords‚ tangents‚ and secants․ Explore central and inscribed angles‚ arcs‚ and related theorems for exam readiness․
A․ Circle Terminology (Radius‚ Diameter‚ Chord‚ Tangent‚ Secant)
Essential Definitions: A thorough understanding of circle terminology is foundational․ The radius is the distance from the center to any point on the circle․ The diameter spans the circle through the center‚ equaling twice the radius․ A chord connects two points on the circle‚ while a tangent line touches the circle at only one point‚ being perpendicular to the radius at that point․
Secant Lines: A secant line intersects the circle at two points․ Distinguishing between these lines is crucial for solving related problems․ Be prepared to identify each element in diagrams and apply their properties to calculate lengths‚ angles‚ and relationships within the circle․ Practice recognizing how tangents and secants interact‚ forming angles and segments that can be analyzed using geometric theorems․ Knowing these terms will unlock more complex circle problems․
Visualizing Concepts: Draw diagrams to solidify your understanding․
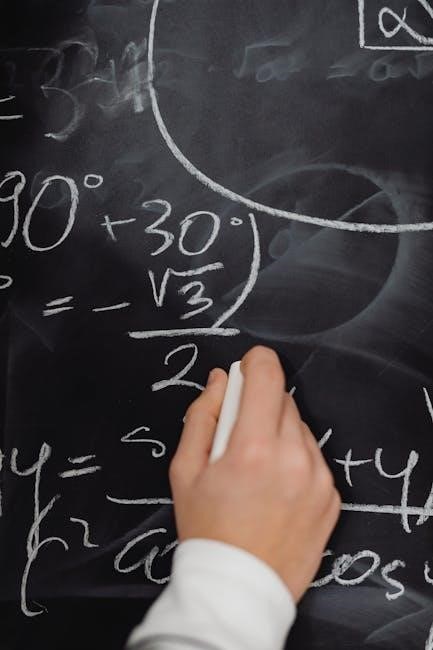
B․ Central Angles and Arcs
Defining the Relationship: A central angle is an angle whose vertex is at the center of the circle․ It directly corresponds to an arc‚ which is a portion of the circle’s circumference․ The measure of the central angle‚ in degrees‚ is equal to the measure of its intercepted arc․ Understanding this fundamental connection is key to solving problems involving arc length and sector area․
Arc Length and Sector Area: Calculate arc length using the formula: (central angle/360°) * 2πr‚ where ‘r’ is the radius․ Sector area is calculated similarly: (central angle/360°) * πr²․ Be comfortable converting between degrees and radians when necessary․ Recognize that a full circle represents 360° or 2π radians․
Practice Problems: Work through various examples to master these calculations and solidify your understanding of the relationship between central angles and arcs․
C․ Inscribed Angles and Intercepted Arcs
Key Concept: An inscribed angle is an angle whose vertex lies on the circle‚ and its sides are chords of the circle․ The intercepted arc is the arc that lies within the inscribed angle․ A crucial theorem states that the measure of an inscribed angle is half the measure of its intercepted arc․
Applications & Theorems: This relationship allows you to determine unknown angle or arc measures․ Understand related theorems‚ such as an inscribed angle intercepting a semicircle is always a right angle (90°)․ Also‚ angles intercepting the same arc are congruent․
Problem Solving: Practice identifying inscribed angles‚ their intercepted arcs‚ and applying the theorem to solve for missing measures․ Be prepared to work with diagrams and utilize logical reasoning․
D․ Circle Theorems and Proofs
Core Understanding: This section tests your ability to apply and prove various circle theorems․ Expect questions involving tangents‚ chords‚ secants‚ and their relationships to angles and arcs․ Mastery requires understanding why these theorems work‚ not just memorizing them․
Essential Theorems: Focus on theorems concerning tangent-chord angles (equal to the intercepted arc)‚ angles formed by intersecting chords‚ and the power of a point theorems (external segment * whole secant = tangent segment squared)․
Proof Strategies: Be prepared to construct formal proofs using given information‚ definitions‚ and previously established theorems․ Practice writing logical arguments and justifying each step․ Diagrams are crucial for visualizing and organizing your proofs․

VI․ Area and Volume
Master formulas! Calculate areas of 2D shapes and volumes of 3D solids – triangles‚ quadrilaterals‚ circles‚ prisms‚ cylinders‚ pyramids‚ and cones are key․
A․ Area of Triangles and Quadrilaterals
Triangles: Recall the fundamental formula: Area = ½ * base * height․ Understand how to identify the base and corresponding height in various triangle types – right‚ acute‚ and obtuse․ Be prepared to apply this formula in problem-solving scenarios‚ potentially involving coordinate geometry to determine base and height lengths․ Don’t forget special cases like equilateral triangles‚ where you might need to calculate the height using the Pythagorean theorem․
Quadrilaterals: Master the area calculations for parallelograms (base * height)‚ rectangles (length * width)‚ and trapezoids (½ * (base1 + base2) * height)․ Recognize that rectangles and squares are special cases of parallelograms․ For more complex quadrilaterals‚ consider dividing them into triangles to facilitate area calculation․ Practice applying these formulas to real-world examples and geometric diagrams․ Understanding the relationship between area and perimeter is also crucial for comprehensive problem-solving․
B․ Area of Circles
Fundamental Formula: The cornerstone of circle area calculation is Area = πr²‚ where ‘π’ (pi) is approximately 3․14159 and ‘r’ represents the radius of the circle․ Ensure you can consistently apply this formula accurately․ A common mistake is using the diameter instead of the radius; remember the radius is half the diameter․
Applications & Variations: Be prepared to solve problems where the radius isn’t directly given․ You might need to derive it from the diameter‚ circumference‚ or other geometric relationships within the problem․ Understand how to calculate the area of sectors (a portion of a circle) and segments (area between a chord and an arc)․ These require understanding central angles and proportions․ Practice converting between radius‚ diameter‚ circumference‚ and area to demonstrate a complete grasp of circle properties․
C․ Volume of Prisms and Cylinders
Core Concept: Volume‚ representing three-dimensional space‚ for both prisms and cylinders is calculated using the formula: Volume = Base Area * Height․ For prisms‚ the base area depends on the shape of the base (triangle‚ square‚ pentagon‚ etc․)․ Cylinders specifically utilize a circular base‚ meaning Base Area = πr²․ Mastering these base area calculations is crucial․
Problem Solving Strategies: Expect problems requiring you to identify the base‚ calculate its area‚ and then multiply by the height․ Be mindful of units – ensure consistency (e․g․‚ all measurements in centimeters)․ You may encounter composite figures‚ demanding you decompose them into simpler prisms or cylinders to determine the total volume․ Practice visualizing these shapes and applying the correct formulas to avoid errors․ Remember to clearly label your work!
D․ Volume of Pyramids and Cones
Key Difference: Unlike prisms and cylinders‚ pyramids and cones have a vertex point‚ impacting their volume calculation․ The formula is Volume = (1/3) * Base Area * Height․ Notice the (1/3) factor – this is essential! The base area calculation remains consistent with prisms (for pyramids) and cylinders (for cones)‚ utilizing shapes like squares‚ rectangles‚ or circles․
Application & Practice: Test questions will likely involve finding the volume given dimensions or working backward to determine missing dimensions (height or radius) when the volume is provided․ Pay close attention to whether the problem describes a pyramid or a cone‚ as the base area formula differs․ Visualizing these three-dimensional shapes and accurately applying the (1/3) factor are vital for success․ Consistent practice is key!